Here you will learn about Travelling Salesman Problem (TSP) with example and also get a program that implements Travelling Salesman Problem in C.
Let say there are some villages (1, 2, 3, 4, 5). To work with worst case let assume each villages connected with every other villages. And there is a Salesman living in village 1 and he has to sell his things in all villages by travelling and he has to come back to own village 1.
He has to travel each village exactly once, because it is waste of time and energy that revisiting same village. This is same as visiting each node exactly once, which is Hamiltonian Circuit. But our problem is bigger than Hamiltonian cycle because this is not only just finding Hamiltonian path, but also we have to find shortest path.
Finally the problem is we have to visit each vertex exactly once with minimum edge cost in a graph.
Brute Force Approach takes O (nn) time, because we have to check (n-1)! paths (i.e all permutations) and have to find minimum among them.
The correct approach for this problem is solving using Dynamic Programming.
Dynamic Programming can be applied only if main problem can be divided into sub-problems. Let’s check that.
Travelling Salesman Problem (TSP) Using Dynamic Programming
Example Problem
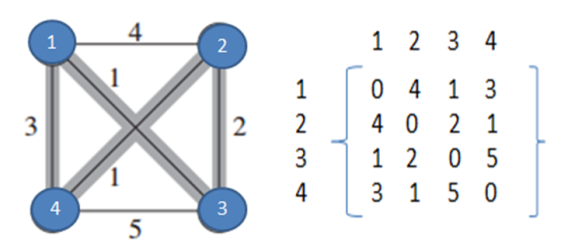
![Travelling Salesman Problem (TSP)]()
Above we can see a complete directed graph and cost matrix which includes distance between each village. We can observe that cost matrix is symmetric that means distance between village 2 to 3 is same as distance between village 3 to 2.
Here problem is travelling salesman wants to find out his tour with minimum cost.
Say it is T (1,{2,3,4}), means, initially he is at village 1 and then he can go to any of {2,3,4}. From there to reach non-visited vertices (villages) becomes a new problem. Here we can observe that main problem spitted into sub-problem, this is property of dynamic programming.
Note: While calculating below right side values calculated in bottom-up manner. Red color values taken from below calculations.
T ( 1, {2,3,4} ) = minimum of
= { (1,2) + T (2, {3,4} ) 4+6=10
= { (1,3) + T (3, {2,4} ) 1+3=4
= { (1,4) + T (4, {2,3} ) 3+3=6
Here minimum of above 3 paths is answer but we know only values of (1,2) , (1,3) , (1,4) remaining thing which is T ( 2, {3,4} ) …are new problems now. First we have to solve those and substitute here.
T (2, {3,4} ) = minimum of
= { (2,3) + T (3, {4} ) 2+5=7
= { (2,4) + T {4, {3} ) 1+5=6
T (3, {2,4} ) = minimum of
= { (3,2) + T (2, {4} ) 2+1=3
= { (3,4) + T {4, {2} ) 5+1=6
T (4, {2,3} ) = minimum of
= { (4,2) + T (2, {3} ) 1+2=3
= { (4,3) + T {3, {2} ) 5+2=7
T ( 3, {4} ) = (3,4) + T (4, {} ) 5+0=5
T ( 4, {3} ) = (4,3) + T (3, {} ) 5+0=5
T ( 2, {4} ) = (2,4) + T (4, {} ) 1+0=1
T ( 4, {2} ) = (4,2) + T (2, {} ) 1+0 = 1
T ( 2, {3} ) = (2,3) + T (3, {} ) 2+0 = 2
T ( 3, {2} ) = (3,2) + T (2, {} ) 2+0=2
Here T ( 4, {} ) is reaching base condition in recursion, which returns 0 (zero ) distance.
This is where we can find final answer,
T ( 1, {2,3,4} ) = minimum of
= { (1,2) + T (2, {3,4} ) 4+6=10 in this path we have to add +1 because this path ends with 3. From there we have to reach 1 so 3->1 distance 1 will be added total distance is 10+1=11
= { (1,3) + T (3, {2,4} ) 1+3=4 in this path we have to add +3 because this path ends with 3. From there we have to reach 1 so 4->1 distance 3 will be added total distance is 4+3=7
= { (1,4) + T (4, {2,3} ) 3+3=6 in this path we have to add +1 because this path ends with 3. From there we have to reach 1 so 3->1 distance 1 will be added total distance is 6+1=7
Minimum distance is 7 which includes path 1->3->2->4->1.
After solving example problem we can easily write recursive equation.
Recursive Equation
T (i , s) = min ( ( i , j) + T ( j , S – { j }) ) ; S!= Ø ; j € S ;
S is set that contains non visited vertices
= ( i, 1 ) ; S=Ø, This is base condition for this recursive equation.
Here,
T (i, S) means We are travelling from a vertex “i” and have to visit set of non-visited vertices “S” and have to go back to vertex 1 (let we started from vertex 1).
( i, j ) means cost of path from node i to node j
If we observe the first recursive equation from a node we are finding cost to all other nodes (i,j) and from that node to remaining using recursion ( T (j , {S-j}))
But it is not guarantee that every vertex is connected to other vertex then we take that cost as infinity. After that we are taking minimum among all so the path which is not connected get infinity in calculation and won’t be consider.
If S is empty that means we visited all nodes, we take distance from that last visited node to node 1 (first node). Because after visiting all he has to go back to initial node.
Time Complexity
Since we are solving this using Dynamic Programming, we know that Dynamic Programming approach contains sub-problems.
Here after reaching ith node finding remaining minimum distance to that ith node is a sub-problem.
If we solve recursive equation we will get total (n-1) 2(n-2) sub-problems, which is O (n2n).
Each sub-problem will take O (n) time (finding path to remaining (n-1) nodes).
Therefore total time complexity is O (n2n) * O (n) = O (n22n)
Space complexity is also number of sub-problems which is O (n2n)
Travelling Salesman Problem in C
#include<stdio.h>
int ary[10][10],completed[10],n,cost=0;
void takeInput()
{
int i,j;
printf("Enter the number of villages: ");
scanf("%d",&n);
printf("\nEnter the Cost Matrix\n");
for(i=0;i < n;i++)
{
printf("\nEnter Elements of Row: %d\n",i+1);
for( j=0;j < n;j++)
scanf("%d",&ary[i][j]);
completed[i]=0;
}
printf("\n\nThe cost list is:");
for( i=0;i < n;i++)
{
printf("\n");
for(j=0;j < n;j++)
printf("\t%d",ary[i][j]);
}
}
void mincost(int city)
{
int i,ncity;
completed[city]=1;
printf("%d--->",city+1);
ncity=least(city);
if(ncity==999)
{
ncity=0;
printf("%d",ncity+1);
cost+=ary[city][ncity];
return;
}
mincost(ncity);
}
int least(int c)
{
int i,nc=999;
int min=999,kmin;
for(i=0;i < n;i++)
{
if((ary[c][i]!=0)&&(completed[i]==0))
if(ary[c][i]+ary[i][c] < min)
{
min=ary[i][0]+ary[c][i];
kmin=ary[c][i];
nc=i;
}
}
if(min!=999)
cost+=kmin;
return nc;
}
int main()
{
takeInput();
printf("\n\nThe Path is:\n");
mincost(0); //passing 0 because starting vertex
printf("\n\nMinimum cost is %d\n ",cost);
return 0;
}Output
Enter the number of villages: 4
Enter the Cost Matrix
Enter Elements of Row: 1
0 4 1 3
Enter Elements of Row: 2
4 0 2 1
Enter Elements of Row: 3
1 2 0 5
Enter Elements of Row: 4
3 1 5 0
The cost list is:
0 4 1 3
4 0 2 1
1 2 0 5
3 1 5 0
The Path is:
1—>3—>2—>4—>1
Minimum cost is 7
Comment below if you found any information incorrect or have doubts regarding Travelling Salesman Problem algorithm.
The post Travelling Salesman Problem (TSP) appeared first on The Crazy Programmer.